Least Square Fitting
Least Square Approximation is the most common way to optimize data fitting.
Before performing a measurement researchers should think about the possible outcomes of their experiment. The create a model to predict the data they expect to measure.
After the measurement as a result you usually get a collection of data points and an equation for your model including some variables. To find the best values for the variables, you first have to define what is “the best”. The least square fitting assumes that the best variables are the ones, where the sum of the residuals square is the lowest. The residuals are the deviations between a measured data point and the predicted value by the model.
In other words: The best values for the variables in the model are the ones, where the simulated data is closest to the measured data.
The most common application in science is the linear regression. However, in electrochemistry especially in Electrochemical Impedance Spectroscopy (EIS) this way of fitting is used to fit a model based on an Equivalent Circuit to the measured data.
Articles
Electrochemical Impedance Spectroscopy (EIS)
Electrochemical Impedance Spectroscopy (EIS) is an electrochemical technique to measure the impedance of a system in dependence of the AC potentials frequency.
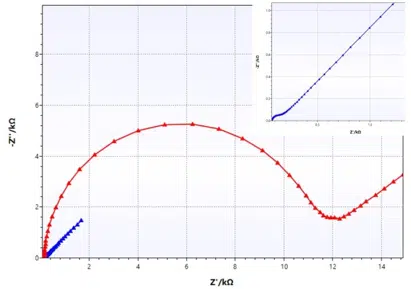
Equivalent circuit fitting for corrosion measurements
In this section of the handbook the Warburg Impedance and the Constant Phase Element (CPE) are introduced, which represent electrochemical effects with no corresponding real electronic components. Furthermore, some equivalent circuits for typical corrosion systems are presented.
